Se você não é lá muito fã de matemática, você deve ter lido o título da matéria e sentido um leve calafrio. No entanto, apesar de a Proporção Áurea ser um conceito matemático, sua aplicação é muito mais abrangente — e fascinante — do que você imagina.
O que é?
Matematicamente falando, a proporção áurea é uma constante real algébrica irracional obtida quando dividimos uma reta em dois segmentos de forma que o segmento mais longo da reta dividida pelo segmento menor seja igual à reta completa dividida pelo segmento mais longo, e seu valor é constituído por 1,6180339887... ou, arredondando, 1,6180. Complicado de entender? Talvez a imagem a seguir ajude um pouco:
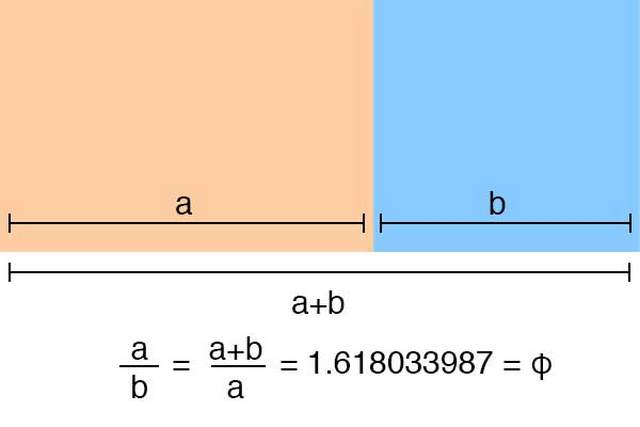
E você reparou que a equação que aparece na parte inferior da figura conta com uma letrinha esquisita? Essa é a letra grega Phi — ou φ —, e a escolha dela para representar a proporção áurea tem a ver com o arquiteto e matemático grego Phidias, que, segundo acredita-se, provavelmente empregou o conceito quando projetou o Parthenon, isso lá no século 5 a.C.
E Phidias não foi o único grego que se tornou fã da proporção áurea! Platão também curtia Phi, e Euclides foi o primeiro a descrevê-la em sua obra “Os Elementos”, há 2,3 mil anos. Depois, no comecinho do século 13, o italiano Leonardo Fibonacci descobriu propriedades únicas em uma sequência de números (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, ...) — dos quais você pode conferir uma representação abaixo:
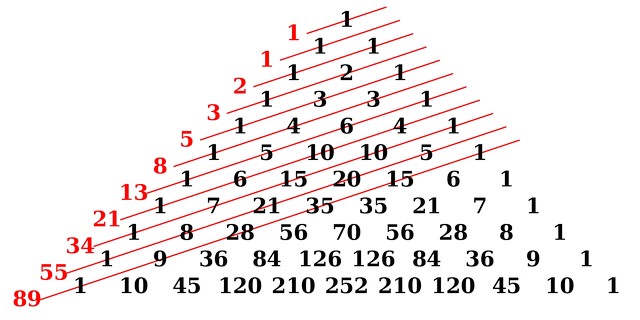
Mais contas
Curiosamente, a sequência de Fibonacci está diretamente relacionada com a proporção áurea, já que a razão entre qualquer par de números sucessivos é bem próxima à proporção áurea. E, conforme os números vão ficando mais altos, a razão se torna cada vez mais próxima de 1,6180. Assim, por exemplo, a razão entre 3 e 5 é 1,666, entre 13 e 21 igual a 1,625, e a razão entre 144 e 233 é 1,618.
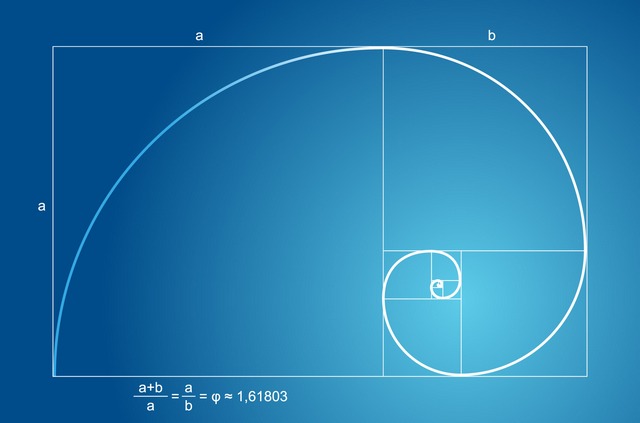
Pois, quando esses números são aplicados às proporções de um retângulo, chegamos ao que em geometria é conhecido como “retângulo de ouro”, e é aqui que a aplicação da proporção áurea começa a se tornar interessante.
Isso porque esse retângulo ficou conhecido como uma das formas geométricas mais visualmente agradáveis que existem; por conta disso, ela teria sido largamente aplicada nas artes e na arquitetura, juntamente com o “espiral áureo” — que é obtido quando desenhamos uma espiral seguindo o fluxo dos quadrados formados no retângulo de ouro. Veja:
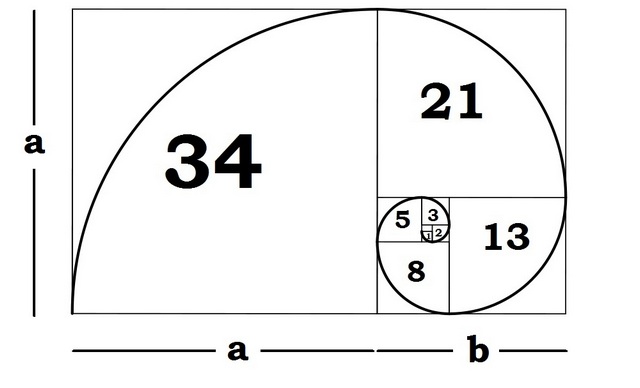
Aplicações
 De Divina Proportione
De Divina Proportione
Dizem que os antigos egípcios empregaram a proporção áurea para construir as Pirâmides de Gizé e, conforme mencionamos anteriormente, os antigos gregos também fizeram uso dela para projetar alguns de seus mais importantes monumentos. E a relação entre a proporção áurea e as artes teria nascido a partir de um livro escrito pelo monge italiano Luca Pacioli chamado “De Divina Proportione” no século 16.
Você sabe o que é a Proporção Áurea?
Luca era amigo de ninguém menos do que Leonardo Da Vinci, e foi ele quem ilustrou o manuscrito do monge. A partir daí, a proporção áurea teria sido aplicada em inúmeros quadros e esculturas da Renascença para que os artistas pudessem alcançar maior beleza e equilíbrio em suas obras.
Aliás, dizem que o próprio Da Vinci teria aplicado o conceito para definir todas as proporções em sua obra “A Última Ceia” e empregado a proporção áurea para criar a “Mona Lisa” e o “Homem Vitruviano”. Além de Da Vinci, outros artistas também teriam feito uso do conceito, entre eles Michelangelo, Botticelli, Raphael, Rembrandt e Salvador Dali. Confira:
Você sabe o que é a Proporção Áurea?
 Há também quem acredite que a proporção áurea tenha se tornado uma ferramenta indispensável para os designers, já que muitos logotipos teriam sido desenvolvidos com base nesse conceito mágico. Mas as aplicações não param por aí...
Há também quem acredite que a proporção áurea tenha se tornado uma ferramenta indispensável para os designers, já que muitos logotipos teriam sido desenvolvidos com base nesse conceito mágico. Mas as aplicações não param por aí...Proporção áurea na natureza

Surpreendentemente, a proporção áurea não se limita a aparecer em obras de arte ou monumentos arquitetônicos. Segundo acreditam alguns, sua abrangência é universal, e ela se reflete na organização dos ossos de humanos e outros animais, na ramificação de veias e nervos, na disposição das pétalas das flores, nos galhos das árvores, na formação de galáxias, na formação de furacões, na geometria dos cristais, nas proporções de compostos químicos e até nas moléculas de DNA.
Você sabe o que é a Proporção Áurea?
No caso das flores, por exemplo, em algumas plantas, o número as pétalas segue a sequência de Fibonacci, e, em outras, as sementes são frequentemente produzidas do centro para as extremidades. Já a forma como os galhos das árvores se ramificam também reflete os números de Fibonacci, assim como os padrões adotados pelas raízes de determinadas algas.
Além disso, as conchas de muitos animais marinhos — bem como as dos caracóis — são perfeitos exemplos do espiral dourado, assim como muitos furacões. Também é possível desenhar o retângulo de ouro sobre as galáxias em espiral. No caso das moléculas de DNA, cada molécula mede 34 x 21 ångströms em cada ciclo completo da dupla hélice, e, na sequência de Fibonacci, os números 34 e 21 são sucessivos.
Existem controvérsias...

Bem, pelo menos no diz que respeito ao emprego da proporção áurea nas artes, na arquitetura e no design, existem controvérsias. Isso porque quem popularizou a ideia de que sua abrangência seria universal foi o psicólogo alemão Adolf Zeising, que, no século 19, propôs a ideia de que a proporção integrava a beleza da natureza e da arte. No entanto, segundo alguns críticos, o problema é que Zeising via linhas e padrões onde eles não existiam.
Nesse sentido, alguns estudos revelaram que nem sempre o retângulo de ouro é o mais esteticamente satisfatório para quem está olhando para um quadro, foto ou edifício. Além disso, apesar de ser uma ferramenta bem conhecida por artistas e designers, de forma geral, ela não é aplicada no desenvolvimento de projetos.
Você sabe o que é a Proporção Áurea?
Estritamente falando, como a proporção áurea é uma constante irracional, não existe nada no mundo real que se encaixe perfeitamente nela. Afinal, assim como é impossível encontrar um círculo absolutamente perfeito na natureza, se aplicarmos a proporção áurea a qualquer objeto de maneira rigorosa, ele sempre ficará um pouquinho fora da medida exata.
FONTE(S)



































Perfeita explicação sobre a Proporção de ouro.
ResponderExcluir